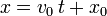MOVIMIENTO PARABÓLICO 

MOVIMIENTO PARABÓLICO
El movimiento parabólico se puede analizar como la composición de dos movimientos rectilíneos distintos: uno horizontal (según el eje x) de velocidad constante y otro vertical (según eje y) uniformemente acelerado, con la aceleración gravitatoria; la composición de ambos da como resultado una trayectoria parabólica.
Claramente, la componente horizontal de la velocidad permanece invariable, pero la componente vertical y el ángulo θ cambian en el transcurso del movimiento.

En la figura 4 se observa que el vector velocidad inicial forma un ángulo inicial respecto al eje x; y, como se dijo, para el análisis se descompone en los dos tipos de movimiento mencionados; bajo este análisis, las componentes según x e y de la velocidad inicial serán:

• v_{0x} = v_0 cos theta_0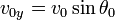

• v_{0y} = v_0 sin theta_0

El desplazamiento horizontal está dado por la ley del movimiento uniforme, por tanto sus ecuaciones serán (si se considera :

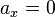
• a_x = 0

• v_x = v_{0x}

• x = v_{0x} t

En tanto que el movimiento según el eje será rectilíneo uniformemente acelerado, siendo sus ecuaciones:

• a_y = -g

• v_y = v_{0y} - gt

• y = y_0 + v_{0y}t - frac{1}{2}g{t^2}

Si se reemplaza y opera para eliminar el tiempo, con las ecuaciones que dan las posiciones e se obtiene la ecuación de la trayectoria en el plano xy:

• y = - frac{g}{2v_0^2 cos^2{theta_0}} x^2 + tan theta_0 x + y_0

que tiene la forma general

• y= a {x^2} + bx + c

y representa una parábola en el plano y(x). En la figura 4 se muestra esta representación, pero en ella se ha considerado (no así en la animación respectiva). En esa figura también se observa que la altura máxima en la trayectoria parabólica se producirá en H, cuando la componente vertical de la velocidad sea nula (máximo de la parábola); y que el alcance horizontal ocurrirá cuando el cuerpo retorne al suelo, en (donde la parábola corta al eje .

Figura 4. Esquema de la trayectoria del movimiento balístico.Objeto disparado con un ángulo inicial desde un punto que sigue una trayectoria parabólica.

MOVIMIENTO RECTILINEO

Figura 1. Variación en el tiempo de la posición y la velocidad para un movimiento rectilíneo uniforme.

Para este caso la aceleración es cero por lo que la velocidad permanece constante a lo largo del tiempo. Esto corresponde al movimiento de un objeto lanzado en el espacio fuera de toda interacción, o al movimiento de un objeto que se desliza sin fricción. Siendo la velocidad v constante, la posición variará linealmente respecto del tiempo, según la ecuación:

• v = v_0 = text{const.} ,

• x = v_0 , t + x_0

donde s la posición inicial del móvil respecto al centro de coordenadas, es decir para

Si La ecuación anterior corresponde a una recta que pasa por el origen, en una representación gráfica de la función tal como la mostrada en la figura 1.

CINEMÁTICA

La 'cinemática' es una rama de la física que estudia las leyes del movimiento (cambios de posición) de los cuerpos, sin tomar en cuenta las causas (fuerzas) que lo producen, limitándose esencialmente, al estudio de la trayectoria en función del tiempo. La aceleración es el ritmo con que cambia su rapidez (módulo de la velocidad). La rapidez y la aceleración son las dos principales cantidades que describen cómo cambia su posición en función del tiempo

La cinemática trata del estudio del movimiento de los cuerpos en general y, en particular, el caso simplificado del movimiento de un punto material. Para sistemas de muchas partículas, tales como los fluidos, las leyes de movimiento se estudian en la mecánica de fluidos.

El movimiento trazado por una partícula lo mide un observador respecto a un sistema de referencia. Desde el punto de vista matemático, la cinemática expresa cómo varían las coordenadas de posición de la partícula (o partículas) en función del tiempo. La función matemática que describe la trayectoria recorrida por el cuerpo (o partícula) depende de la velocidad (la rapidez con la que cambia de posición un móvil) y de la aceleración (variación de la velocidad respecto del tiempo).

El movimiento de una partícula (o cuerpo rígido) se puede describir según los valores de velocidad y aceleración, que son magnitudes vectoriales.

SISTEMA DE COORDENADAS

En el estudio del movimiento, los sistemas de coordenadas más útiles se encuentran viendo los límites de la trayectoria a recorrer, o analizando el efecto geométrico de la aceleración que afecta al movimiento. Así, para describir el movimiento de un talón obligado a desplazarse a lo largo de un aro circular, la coordenada más útil sería el ángulo trazado sobre el aro. Del mismo modo, para describir el movimiento de una partícula sometida a la acción de una fuerza central, las coordenadas polares serían las más útiles.
En la gran mayoría de los casos, el estudio cinemático se hace sobre un sistema de coordenadas cartesianas, usando una, dos o tres dimensiones según la trayectoria seguida por el cuerpo.